Pensando nos jogos de infância, outro dia lembrei do “cai-não-cai”, lançado pela Estrela por aqui em meados dos anos 1970 e que ainda é vendido nesse século, ainda que existam várias dicas para o mesmo brinquedo com materiais recicláveis. A ideia é simples, como pode-se ver na ilustração. Uma trama de varinhas impede que as bolinhas de gude na parte superior do recipiente caiam para a parte de baixo. O desafio para cada jogador é, ao retirar uma vareta na sua vez, deixar cair o menor número possível de bolinhas. Quem já jogou sabe que, a cada pauzinho retirado, vão caindo uma ou outra bolinha, até que, de repente, puxando uma vareta todas as restantes lotam a parte de baixo do recipiente. O que acontece nesse jogo? As varetas formam uma trama na qual todas as bolinhas se sustentam inicialmente. Ao retirar aos poucos essa trama, as bolinhas de gude se rearranjam, movendo-se através de canais que se formam, outras passam por tudo e caem. Com a trama cada vez mais precária, abrem-se passagens para que todas as bolas restantes caiam de uma vez e o jogo acaba no que se chama de percolação[I]
É o mesmo fenômeno que observamos quando a água quente derramada no coador encharca todo o pó de café, antes de cair no bule. Aliás, foi aí que a palavra percolação apareceu no começo do século XIX, no ensaio de Sir Benjamin Thomson (1753-1814), conhecido também como conde Rumford, um dos pais da Termodinâmica e amante do café: “Sobre as excelentes qualidades do café. Nesse ensaio o cientista descreve a cafeteira que inventou, o “percolador de café”, e seus parâmetros de uso[II]
Apesar de ser um fenômeno cotidiano – observado tanto ao passarmos um café, quanto ao irrigarmos um vaso de plantas até que a água escorra no fundo - apenas no século XX a percolação começou a ser estudada mais sistematicamente, rumo a uma teoria. Um marco nessa história é uma colaboração nos anos 1950 entre os matemáticos britânicos John Hammersley (1920-2005) e Simon Broadbent (1928-2002), iniciada quando o primeiro apresentava um trabalho em um congresso e o segundo comentou que o método apresentado poderia ser aplicado a um problema interessante: dado uma rede regular de poros, conectados com uma certa probabilidade (ou seja, alguns estão conectados, outros não), qual proporção dessa rede seria preenchida por um gás introduzido nesses poros? Assim surgiu o que é considerado o primeiro artigo sobre teoria da percolação em 1957[III]. A aplicação inicial em mente era bem específica: melhorar o funcionamento de máscaras de gás para a segurança de mineiros, mas os desdobramentos “percolariam” em várias áreas do conhecimento. Nesse artigo, consideraram vários exemplos, entre eles um sobre a propagação de uma epidemia em um pomar. O modelo era simples, mas muito útil e funciona em várias situações. As árvores de um pomar eram colocadas nos nós de uma rede quadrada. Cada uma das quatro árvores mais próximas de uma dada árvore infectada teriam uma probabilidade p de também ser infectadas. E a pergunta de pesquisa: um número grande de árvores seriam infectadas (a tal percolação) ou a epidemia ficaria localizada em apenas uma parte do pomar? Tudo depende da tal probabilidade p, associada à distância entre as árvores. Então outra pergunta: haveria uma “probabilidade crítica”, acima da qual todas as árvores seriam infectadas? Na prática, para o agricultor, seria o compromisso entre produção de frutas (que aumenta com a diminuição da distância entre as árvores) e a segurança fitossanitária (que, em sentido oposto, aumenta com a distância).
A investigação desse problema fascinante se intensificou com o uso de computadores, que começaram a ser usados na mesma época, para simulações numéricas. Hoje existem várias simulações disponíveis pela web para que brinquemos assim, em vez de com bolas e varetas. Os resultados de uma dessas simulações[IV] estão ilustrados aqui, também para uma rede quadrada, como a proposta para o pomar dos matemáticos britânicos, mas com algumas diferenças.
Os quadradinhos vermelhos são aqueles que podem ser alcançados do topo ou da base, passando apenas por quadradinhos preenchidos. Os números abaixo das figuras representam a probabilidade de preenchimento. Vejam que os azuis estão preenchidos, mas não estão em contato, nem com o topo, nem com a base. Se aumentamos o número de quadrinhos preenchidos de 0,3 (30%) para 0,5 (50%), os caminhos em vermelho avançam um pouco para dentro do campo maior e algo acontece para 0,6(60%): o chamado “limiar de percolação” é alcançado e podemos ligar o topo à base passando apenas por quadradinhos vermelhos. Nesse exemplo específico da simulação, os quadradinhos vermelhos não “infectam” os vizinhos azuis que restam, como em um pomar, mas podemos pensar numa outra simulação onde isso acontece.
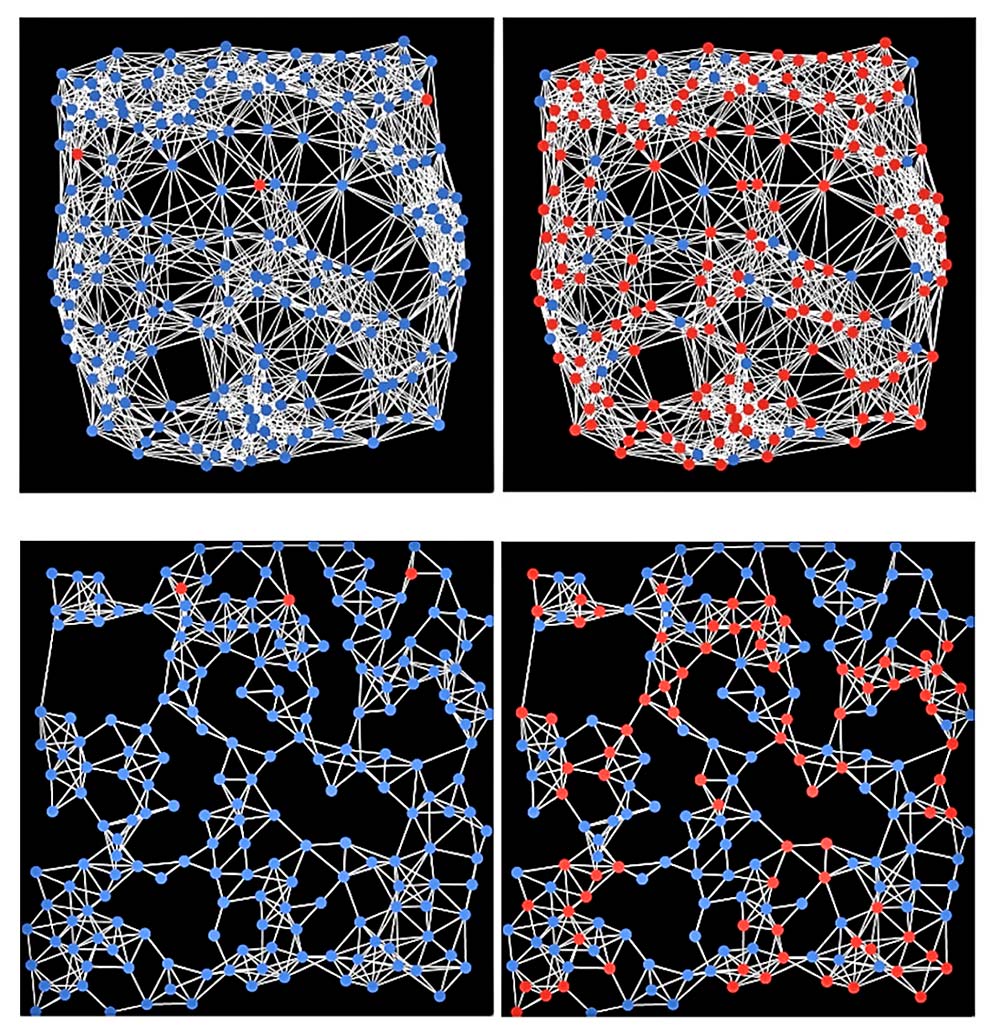
Uma evolução de infectados pode ser visualizada, por exemplo, na simulação do Observatório Covid-19 BR[V], que em vez de uma praga em um pomar, considerou pessoas em contato com outras e com uma certa probabilidade de um infectado infectar outros. As redes não são quadradas, têm esse aspecto mais irregular das relações humanas: uns tem mais contatos que outros. Nas duas redes são consideradas 200 pessoas, mas na primeira o número médio de contatos é de 18 para cada pessoa, na segunda é de 6, devido a um certo distanciamento físico recomendado. O código de cores é o mesmo: vermelho para infectados e azuis para pessoas sem o vírus. Quando o contato é menor, apenas parte da população é infectada, mas no caso sem isolamento, com o passar do tempo, a epidemia percola rapidamente, embora nem todos estarão infectados ao mesmo tempo, devido a uma probabilidade de cura introduzida no modelo. A ilustração aqui é para o “antes” (com três infectados iniciais em ambas as situações) e o “depois” em cada caso.
Os exemplos acima são todos da tal percolação, mas cada uma com sua peculiaridade. No caso do café, um grãozinho do pó que se molha, não seca enquanto passamos o café. Na rede de pessoas numa epidemia, alguém pode eliminar o vírus, mas depois corre o risco de se reinfectar. Nesses exemplos, junto com o pomar do artigo de 1957, temos o que se chama de percolação por ligação, a água quente e os contágios vão encontrando ligações para se expandir. Na simulação com os quadradinhos, cada imagem é um sorteio de probabilidade de preencher um quadradinho ou não e fica assim, não muda com o tempo. É o que os especialistas chamam de percolação por sítio. É preciso juntar esses exemplos todos para pensar em um outro: e se os quadradinhos do exemplo que não muda com o tempo começassem a contaminar também, de alguma forma, os vizinhos e o sistema passasse a mudar com tempo também? E vamos pensar ao contrário: um quadradão vermelho todo preenchido inicialmente. Preenchido por árvores, como numa floresta, por exemplo. Agora vamos desmatando aos poucos os quadradinhos, que grudados uns aos outros representam áreas maiores desmatadas. E as bordas das áreas desmatadas podem avançar, afetando (“contaminando”) glebas vizinhas. Chega uma hora que a floresta deixa de “percolar” e o avanço do desflorestamento talvez não possa mais ser detido. É o que preveem esses modelos de percolação, que podem ser comparados aos padrões de áreas preenchidas, como as da ilustração dessa coluna, ou desmatadas, como na pesquisa realizada por um grupo de pesquisa alemão e publicado na revista Nature em 2018: “Padrões globais de fragmentação de florestas tropicais”[VI]
A repercussão sobre essas observações, principalmente sobre qual seria o “limiar de percolação”, acima do qual podemos perder tudo, é intensa e o debate é acirrado dentro da comunidade científica. Não devemos, no entanto, pensar em esperar por uma resposta definitiva, comprovada observacionalmente, pois nosso planeta não é uma simulação como as que ilustram esse texto. E percolações ocorrem, como vimos aqui. Pense nisso quando for passar o próximo café.
Esse texto não reflete, necessariamente, a opinião da Unicamp.
[I] Essa coluna é uma continuação do tema redes discutido anteriormente: https://www.unicamp.br/unicamp/ju/artigos/peter-schulz/ligando-os-pontos-da-pandemia
[II] Para um breve História do café, cafeteiras e coadores: https://blog.locafe.com.br/coadores-de-cafe-uma-invencao-de-fabricacao-de-cafe-vintage-ainda-em-demanda/
[III] Nicolas Bacaër, Percolation and epidemics (1957) in A short history of MAthematical Population Dynamics, Springer, p 121-126 (2011).
[IV] Wolfram demonstrations Project: https://demonstrations.wolfram.com/PercolationOnASquareGrid/
[V]https://guimaraeslabbr.weebly.com/COVID19.html (acessado em 6/10/2020)
[VI] Franziska Taubert e colaboradores, Nature vol. 554, p. 519-522 (2018): https://www.nature.com/articles/nature25508
