Modelo matemático auxilia na análise prognóstica de câncer nos rins
Dissertação de mestrado desenvolvida por Cristina Sacilotto junto ao Departamento de Matemática Aplicada, do Instituto de Matemática, Estatística e Computação Científica (Imecc) da Unicamp, orientada pelo professor Laércio Luis Vendite, apresenta a construção de dois modelos matemáticos desenvolvidos para predizer os riscos de metástase e de morte em pacientes portadores de câncer nos rins do subtipo mais comum, denominado convencional, caracterizado por células claras.
O carcinoma de células renais é uma doença heterogênea com prognóstico amplamente variável e responsável por 2% das neoplasias malignas. O diagnóstico mais preciso do risco de progressão da doença e da mortalidade após o tratamento é essencial para orientação de pacientes, tomada de decisões no tratamento e seleção de seguimentos adequados. No Brasil, as neoplasias constituem a segunda causa de morte, superada apenas pelas doenças do aparelho circulatório.
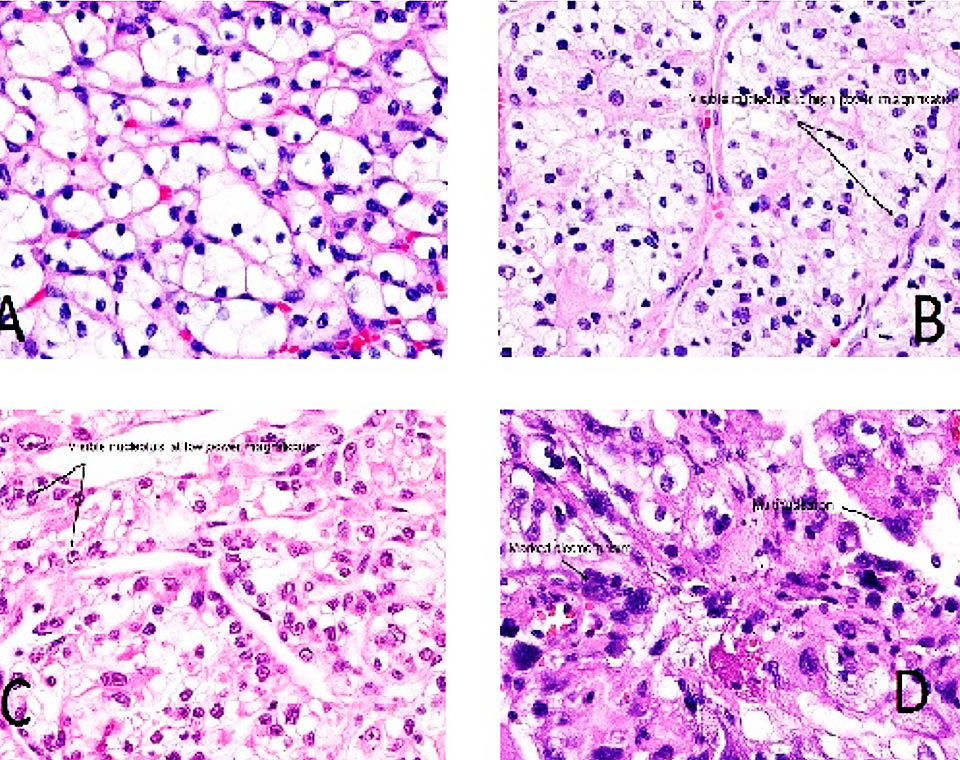
Como a discussão e compreensão dos fatores que determinam os prognósticos de tumores renais são fundamentais para o estabelecimento de sua abordagem, a pesquisa analisa alguns deles e suas importâncias na sobrevida dos pacientes. Hoje se utiliza, com considerável valor prognóstico, o Sistema de Graduação de Fuhrman, que classifica o padrão nuclear da neoplasia em quatro graus, determinados em função da diferença entre o núcleo celular de uma célula cancerosa e uma sadia. Os tumores de grau 1 são considerados com prognóstico favorável, os de grau 4 com prognósticos sombrios e intermediários, os de graus 2 e 3. Entretanto, na comunidade médica, existe um questionamento em relação a essa classificação que se mostra incompatível em relação a determinados casos reais, sugerindo que não basta levar em consideração apenas o grau de comprometimento das células para o diagnóstico.
Disponível em: https://www.auanet.org/education/modules/pathology/kidneycarcinomas/fuhrman-grade.cfm
O estudo, além de uma análise desse critério univariado, considera também outros fatores, do que resulta uma análise multivariada, de forma que, ao combiná-los com a classificação de Fuhrman, possam conduzir a resultados mais precisos para o prognóstico da neoplasia, permitindo verificar a relação entre o grau de Fuhrman e a sobrevida. Os avanços nos diagnósticos e tratamentos e o impacto que podem gerar na sobrevida dos pacientes são relevantes para a definição prognóstica em indivíduos com a doença. A intenção da pesquisa é a de auxiliar o especialista na tomada de decisões com relação ao estádio da neoplasia.
Modelo matemático
Na verdade qualquer sistema de graduação aceito hoje na prática patológica, como o de Fuhrman, apresenta certo grau de subjetividade, pois as doenças geralmente são descritas em termos linguísticos, que são vagos, difíceis de traduzir quantitativamente. Daí a vantagem de um modelo matemático, como o que utiliza a Teoria dos Conjuntos Fuzzy, utilizada em situações duvidosas e de incerteza. Essa teoria associa a precisão da matemática e as impressões do mundo real, de modo que os dados incertos e a opinião dos especialistas sejam levados em conta e incorporados aos modelos matemáticos.
A propósito, a pesquisadora afirma: “A subjetividade das informações no estudo do câncer renal nos motivou a utilizar a Teoria dos Conjuntos Fuzzy para tratar o problema. Diante das incertezas das informações, cremos que o uso dessa teoria é apropriado. Trata-se de uma linguagem do pensamento lógico, cada vez mais necessária à área de saúde”.

Com efeito, na literatura matemática encontram-se vários trabalhos que utilizam a teoria de conjuntos fuzzy para analisar eventos biológicos, em particular neoplasias. Os modelos matemáticos desenvolvidos têm contribuído amplamente para maior compreensão das ocorrências médicas, seus diagnósticos, prognósticos e para a eficiência dos tratamentos.
O trabalho faz parte da linha de pesquisa do professor Laércio que, há quase trinta anos, se dedica à biomatemática, e teve como referências estudos sobre o câncer da próstata e da bexiga também orientados por ele. Seu foco foi a construção de dois modelos matemáticos fuzzy para predizer os riscos de metástase e morte para indivíduos com tumores renais e analisar a relação entre a graduação de Fuhrman e o prognóstico de pacientes com essa neoplasia.
O modelo fuzzy utilizado para prever o risco de metástese combina os dados do tumor do paciente - grau de Fuhrman, presença de necrose, tamanho do tumor e estadiamento, ou seja, o estado clínico do paciente, que depende das ponderações passadas por clínicos. Já o modelo utilizado para a previsão de morte utiliza os mesmos dados do primeiro modelo trocando apenas o fator tamanho do tumor pela presença de metástase. Os dois modelos valem-se de um conjunto de regras, de natureza linguística, elaboradas a partir da ajuda de especialistas, de pesquisas em literatura da área e em dados estatísticos de pacientes do Hospital de Clínicas (HC) da Unicamp. A análise estatística desses dados permitiu identificar as variáveis mais determinantes a serem consideradas, como a presença de necrose e estadiamento, contribuindo para o ajuste dos pesos das regras estabelecidas para cada modelo. “Criamos regras com as informações dos especialistas com os pesos atribuídos e suporte da análise estatística”, esclarece o docente.

Por fim, foram realizadas simulações com os dados colhidos dos pacientes do HC para verificar a compatibilidade do modelo com a realidade. De acordo com a pesquisadora, os resultados podem ser considerados satisfatórios e compatíveis com o observado nos pacientes reais.
Os pesquisadores consideraram de fundamental importância no desenvolvido do trabalho as colaborações dos urologistas Ubirajara Ferreira e Wagner Eduardo Matheus; dos patologistas Athanase Billis e Larissa Eloy; e do médico residente Eduardo Azevedo, todos do HC da Universidade.
Ponderações
Os modelos foram testados em situações concretas de pacientes brasileiros, com histórico conhecido. Devidamente operacionalizados eles fornecem ao médico informações em termos de possibilidade e não probabilidade, não exigindo portanto um grande banco de dados para indicar as chances do tumor desenvolver metástase e de sobrevida do indivíduo.
O modelo fornece ao clínico o melhor diagnóstico possível em dado momento. Laercio explica: “Hoje o médico faz o diagnóstico baseado nas evidências médicas e em suas experiências. Nosso trabalho formaliza e organiza essas evidências, facilitando um diagnóstico preciso e, em consequência, um tratamento mais adequado. Como o modelo é construído com base nas informações de especialistas, incorpora as experiências médicas e o software construído com base nele fornece respostas segundo os conceitos clínicos”.
Para a pesquisadora o modelo proposto permite um diagnóstico mais preciso em relação à evolução do tumor. Mas como as conclusões decorrem da utilização do banco de dados do HC da Unicamp, ela faz um alerta: “Como simulações atêm-se a um universo restrito, há necessidade de novos experimentos para que os resultados sejam confirmados e sedimentados”.
O professor Laércio conclui: “É importante que este tratamento matemático seja debatido pela comunidade médica, pois nosso procedimento não encontra paralelo em outras pesquisas de repercussão internacional. Comprovamos, através de um modelo matemático, que existem indícios muito fortes de que a classificação de Fuhrman tem alcance limitado”.